[ロードスターで考える] 走行抵抗の2大要素とは? 街乗り/高速でそれぞれ気をつけること

車が走ろうとする力を阻害する「抵抗力」について紐解いてみましょう。
一般人向けにちゃんと解説されているものがあまりありませんからね。計算が多くて退屈かもしれませんがお付き合いください。
題材には、マツダ・ロードスター(4代目ND型)と、兄弟車のアバルト・124スパイダーを使います。同じ車体ながら性格がまるで違うのが見えてきますよ。
目次
走行抵抗の要素は主に2つ
ニュートラルギアで走っている車は、何の抵抗力も無ければそのままの速度で走り続けます(等速度運動)。でも実際は徐々に減速していきますよね。走行抵抗があるからです。ボールが氷の上を低速で転がるような場合は抵抗はほとんど無視できますが、車の場合は無視できないほど大きな走行抵抗が発生しています。
走行抵抗には主に2つあります。
空気抵抗
まず空気抵抗です。地球上で移動する上で空気抵抗は避けて通れません。
空気抵抗は速度が上がるほど大きくなります。速くなるほど抵抗が大きくなるので、どこかでエンジンパワーより大きくなってしまいます。そこがその車の最高速度です。
空気抵抗は速度だけでなく車体のカタチにも影響を受けます。乗用車よりバスやトラックのように車体が大きいほど空気抵抗が大きくなりますし、ミニバンよりスポーツカーのように滑らかな形の方が空気抵抗が小さくなります。同じエンジンを積んだ車でも最高速度が違うのはカタチが理由です。
転がり抵抗
車が地面と接触して走行する以上、タイヤと地面の間に抵抗が発生します。アスファルトの上を転がるゴムタイヤには転がり抵抗が発生します。
転がり抵抗は速度には関係なく、タイヤにかかる荷重に依存します。つまり、ほぼ車両重量に依存しています。軽い車ほど転がり抵抗は小さいです。
空気抵抗が速度依存なので高速域では空気抵抗の方が大きくなりますが、低速域ではほぼ転がり抵抗のみになります。
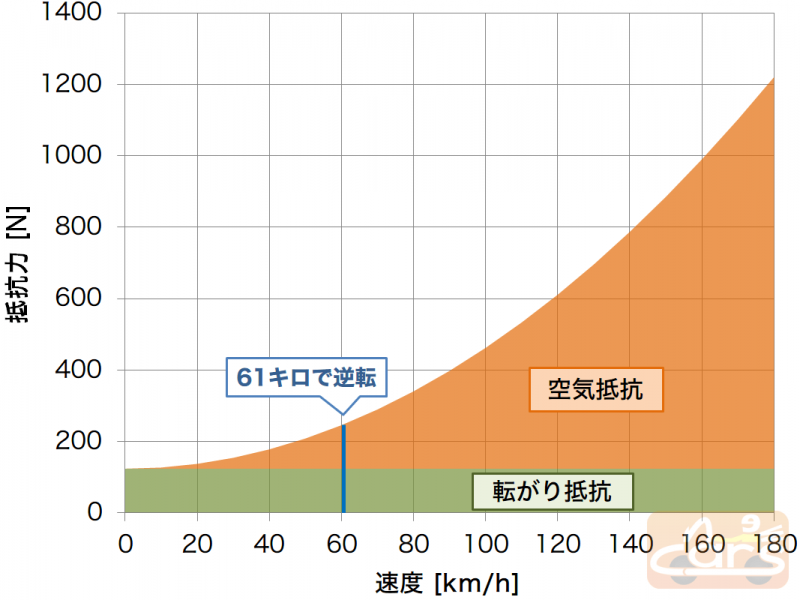
速度が上がると空気抵抗がぐんぐん増えていきますね。ロードスターの場合、61km/hで大小が逆転します。
他の抵抗
他には、加速時にギアやタイヤの回転速度を変化させる際の慣性抵抗、坂を上る際の勾配抵抗(下る場合はマイナス)があります。0-100km/h加速の計算など、加速を考える場合は慣性抵抗も無視できません。
現在カタログに書かれているエンジン仕様(ネット値)は、エンジン+補機類での数値です。実際にタイヤに伝えられるまでには、トランスミッションやデフを通るので、ロスが発生します。この駆動系ロスも、考え方によっては抵抗と見なせます。
今回の抵抗力の解説では勾配や加減速時については扱いません。駆動系ロスについては別途最高速度の計算で紹介します。
空気抵抗
空気抵抗は、以下の式で表されます。
$$F=\frac{1}{2}\rho\,C_{D}\,S\,V^2 $$
- \(\rho\) は空気密度。地上では 1.225 kg/m3 とするのが一般的。
- \(C_{D}\) は空気抵抗係数。車体の形状によって変わる。0.25~0.60 くらいの範囲にほとんどの車が入る。
- \(S\) は前面投影面積。車体を正面から見たときの面積。m2。
- \(V\) は速度。m/s。
ロードスターの場合、残念ながら空気抵抗係数や前面投影面積について公式に紹介されている数字はありません。
空気抗力係数
空気抵抗係数について明確な数字は分かりません。ただ、開発者陣の発言や過去のデータから推測するに、0.30~0.35くらいの値になっていると思われます。ここでは0.34とします。
前面投影面積を求める
前面投影面積は、三面図からPhotoshopの機能を使って求めましょう。
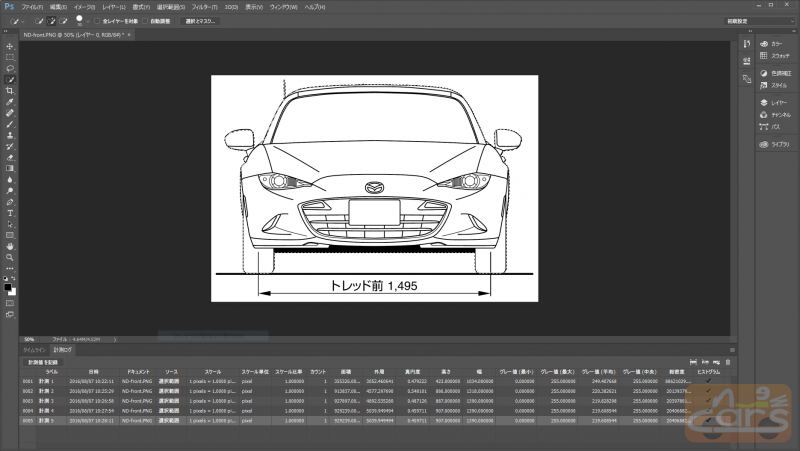
表記されているフロントトレッドは1.495m。これは画像上では1,088ピクセルでした。車体の面積はPhotoshopによると 929,239 なので、
$$ 929239\times \left(\frac{1.495}{1088}\right)^2=1.754\,\mathrm{m^2}$$
となり、1.754 m2 だと分かりました。
空気抵抗の計算
先ほどの式に数字を入れてみましょう。
$$F=\frac{1}{2}\times 1.225\times 0.34\times 1.754\times V^2$$
$$=0.3653\,V^2\,\mathrm{[N]}$$
となります。速度Vを m/s ではなく km/h で表す場合は、\(F=0.02818\,V^2\,\mathrm{[N]}\) となります。
例えば 100 km/h のときは、
$$F=0.02818\times 100^2=281.8 \mathrm{[N]}$$
となります。
空気抵抗の他の要素
空気抵抗にはボディ形状の他にも、エンジンルーム内の冷却系やエアコンなどによる抵抗もあります。これらは \(C_{D}\) 値には含まれません。車両全体の空気抵抗の20%程度はボディ以外の抵抗だと言われています。
正確な値は分かりませんが、後ほど検証する最高速度や0-100km/h加速に照らし合わせると、\(C_{D}\) 値による空気抵抗に20%上乗せするとちょうど良いようです。
転がり抵抗
タイヤが転がるとき、タイヤはわずかに変形しています。その変形で失われるエネルギーが転がり抵抗です。タイヤにかかる荷重が大きいほど転がり抵抗が大きくなりますが、回転速度が速くなっても転がり抵抗は変化しません。
転がり抵抗は以下の式で表されます。
$$F=C_{rr}\,W$$
- \(C_{rr}\) は転がり抵抗係数。タイヤによって決まる。
- 自動車用タイヤの転がり抵抗係数は6.2~15(×10-3)。
- \(W\) はタイヤにかかる荷重。N。
転がり抵抗係数
転がり抵抗係数はタイヤのサイズや銘柄によって決まります。昨今「エコタイヤ」と呼ばれているものは、(グリップ性能と引き替えに)転がり抵抗係数が低いものを指します。
転がり抵抗係数は燃費への影響が大きいこともあって、統一した評価指標が明記されています。転がり抵抗の評価指標は以下の通り。
| 転がり抵抗係数(RRC 10-3) | 評価 |
|---|---|
| RRC≦6.5 | AAA |
| 6.6≦RRC≦7.7 | AA |
| 7.8≦RRC≦9.0 | A |
| 9.1≦RRC≦10.5 | B |
| 10.6≦RRC≦12.0 | C |
ロードスターに標準装着されているタイヤは「ADVAN Sport V105」です。ヨコハマタイヤのサイトでデータを見てみると、転がり抵抗評価はCか無印のいずれかです。
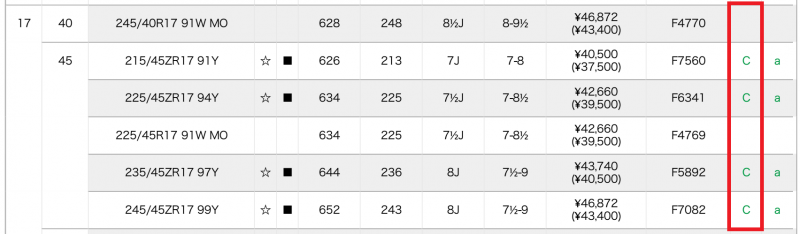
この表から推測するに、おそらくすべて「C」でしょう。なぜなら、無印になっているものはウェットグリップ性能も無印、Cと記入されているものはウェットグリップが最高評価のaです。とすると、無印のものは評価していないだけだと思われます。
Cなら10.6~12.0の間ですね。中央値をとって11.3とします。すべて 10-3 の数値なので、\(C_{rr}=0.0113\) です。
タイヤにかかる荷重
タイヤ4輪が車体の重量を分担して支えていますが、転がり抵抗はすべて同じ向き(進行方向逆向き)なので、車両全体の転がり抵抗はタイヤ1輪に全荷重がかかっているとしても求められます。
タイヤにかかる荷重は、車の重さと、ダウンフォース(あるいは揚力)による荷重です。ただ、車の重量に対して揚力による荷重は小さい(100km/hでも数%程度)なので今回は無視します。
車両の重量は、カタログに記載されている車両重量に、乗員二人分に当たる110kgを加えたものとします。ロードスターの場合は、SスペシャルパッケージのMTで\(1010+110=1120\,\mathrm{kg}\)です。荷重は \(1120\times 9.8=10976\,\mathrm{N}\) となります。
転がり抵抗は一定値
$$F=0.0113\times 1120\times 9.8=124.0\,\mathrm{N}$$
となります。速度に関わらず、常に一定値124Nの抵抗となっているわけですね。
街中では転がり抵抗、高速では空気抵抗
各速度での抵抗値は以下のようになります。
| 速度 | 転がり抵抗 | 空気抵抗 |
|---|---|---|
| 20 km/h | 124 N (90 %) |
14 N (10 %) |
| 60 km/h | 124 N (50 %) |
122 N (50 %) |
| 100 km/h | 124 N (27 %) |
338 N (73 %) |
| 140 km/h | 124 N (16 %) |
663 N (84 %) |
| 180 km/h | 124 N (10 %) |
1,096 N (90 %) |
街中を走るなら、荷物 と 空気圧 に注意!
街中を走る速度域では、転がり抵抗の影響の方が大きいです。
転がり抵抗を決めるのは、車重とタイヤ銘柄。街中で抵抗値を低くする(=燃費と走りを良くする)には、軽い車に転がり抵抗の小さいタイヤを組み合わせると良いということが分かりますね。
今ある車&今履いているタイヤの場合はどうすればいいでしょうか? 注意すべきは荷物と空気圧です。
重いほど転がり抵抗が大きくなるので、車内に無駄な荷物が載っていると転がり抵抗が増加します。重いゴルフバッグや工具類は下ろしましょう。軽くなると加速が良くなる(別記事で解説します)ので、加速時のアクセル開度が小さくなって加速中の燃費が良くなるという側面もあるので、重さは非常に効果的です。軽さという面では無意味に小さなモーターを積んだハイブリッドはどうかと思います。
転がり抵抗では、空気圧に注意しましょう。先ほど出てきた転がり抵抗係数は、適正空気圧の場合の値です。空気圧が下がれば設置面積が増えて、転がり抵抗が大きくなります。逆に空気圧を上げると転がり抵抗は小さくなります。
でもむやみに空気圧を上げるとグリップ力が低下してスリップしやすくなるので危険です。高速道路を走らない場合、適正空気圧より1割程度までなら上げても問題無いでしょう。街乗り中心なら空気圧をこまめにチェックするのが大事です。
高速を走るなら、車の大きさ・カタチ と 速度 に注意!
高速走行時は、空気抵抗の方が重要になってきます。空気抵抗を決めるのは、車のカタチ、前面投影面積、速度の3つです。
$$[空気抵抗]\,=\,[空気抵抗係数]\,\times\,[前面投影面積]\,\times\,[速度]^2$$
最も影響が大きいのは速度です。速度は2乗で効いてくるので、速度を上げると急激に空気抵抗が増加します。車にかかる抵抗全体は、80キロに比べて120キロでは1.8倍、140キロでは2.3倍にもなります。80キロを120キロにすれば移動速度は1.5倍ですが、ガソリンは2.7倍のペースで無くなっていきます。不必要に速度を上げるのはガソリンを空気中に捨てているのと同じです。
同じ速度の場合、空気抵抗は車の大きさと形に依存します。形は箱型の方が抵抗が大きく、新幹線のような流線型になるほど抵抗が小さいです。大きさは単純で、車を正面から見たときの面積が大きいほど空気抵抗が大きいです。
正面から見た図を、縮尺を同じにして比べてみましょう。
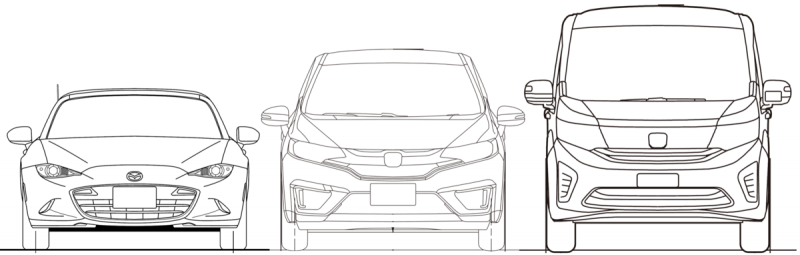
ロードスター,フィット,ステップワゴン
| ロードスター | フィット | ステップワゴン | |
|---|---|---|---|
| 前面投影面積 (フィットに対する割合) |
1.7 m2 (78 %) |
2.2 m2 (100 %) |
2.8 m2 (124 %) |
形のことを考慮せずとも、いかにミニバンの空気抵抗が大きいかが分かると思います。そしてロードスター(幌閉め)の方がステップワゴンより空気抵抗が小さい形状なのは明らかです。おそらくステップワゴンはロードスターの2倍以上の空気抵抗があると思います。
高速走行中には、エンジンの力はほとんど空気抵抗、つまり空気とボディをちょっとだけ暖めるために使われます。その上車体が大きく箱型のミニバンやSUVはそもそも空気抵抗が大きいですね。高速を無駄にかっ飛ばしてるミニバンを見かけたら、「ガソリンを無駄に使って空気の壁にぶつかってるんですね、ご苦労様」と生暖かい目で見守りましょう。
まとめ
今回は車にかかる2大抵抗力、空気抵抗と転がり抵抗について詳しく解説しました。
前回の駆動力の話と合わせると、最高速度を計算で求めることができます。次回は最高速度を計算してみましょう。